The Stewart-Gough Platform Manipulator - Hexapod
1. A brief description of Stewart-Gough platform
This article presents only a review of the Stewart-Gough platforms and includes quotations from the literature.
The Stewart-Gough Platform (SGP) is a 6 degrees of freedom parallel manipulator. There are a plethora of published studies in the literature on the subject of Stewart platforms or parallel manipulators in general (Merlet, 2006; Stewart, 1965; Liu, Li, & Li, 2000; Jakobovic & Jelenkovic, 2002; Lenarčič & Wenger, 2008; Guo & Li, 2006; Mukherjee, Dasgupta, & Mallik, 2007; Gürenci, Sarigül, & Karagülle, 2007; Lee & Geng, 1993; Gogu, 2008), perhaps starting with Stewart original paper (Stewart, 1965). Nonetheless in this article a brief review of the subject is offered.
In fact SGP is the representative case of parallel manipulators (Mruthyunjaya & Dasguptaa, 2000). They have a fixed base, which is connected to a mobile platform by six legs (called struts) with adjustable lengths, as illustrated in Figure 1 . The joints connecting the struts to the plates are normally ball and socket or universal joints. The mobile platform is also called end effector or simply effector, motion of which is controlled by the lengths of the struts. Since there are six parameters defining a motion is space, there is no redundancy in the system and it is statically is determinant, although additional legs can be included, as will be discussed later. Having only six length parameters to define the positions and motion of the system is clearly an advantage for the clinical usage by surgeon and patient. Nevertheless, it is posing a rather complex problem of finding the parameters that are required to define the position/motion of a rigid body relative to any (fixed) coordinate system, namely three angles of rotation and three translational coordinates.
SGP can be considered as a parallel robot, in contrast to the regular serial robots. The reason is that while in serial robots arms are connected to form an open kinematic chain, in SGP, the (six) arms (or legs) are all used to connect the base to the mobile platform, forming a closed kinematic chain.
The origin of the term robot can be found in a science fiction play written by Karel Čapek (1920). The play titled R.U.R. was published in Czech in 1920 as an abbreviation of Rozum's Universal Robots. It was a collective drama with a comic prologue and three acts and was first performed in National Theatre in Prague on January 25, 1921. In Czech language “rozum” means wisdom and “robota” means servitude/forced labour/drudgery. Since the word robot was apparently coined by the author's brother, cubist painter and writer Joseph Čapek, the term has since been used to refer to a wide range of man-made tools from devices to programs which are used to perform various tasks automatically and autonomously by replacing humans (Gogu, 2008).
Structurally speaking, SGP offers the following distinctive advantages over its serial counterparts (Merlet, 2006; Mruthyunjaya & Dasguptaa, 2000; Dasgupta & Mruthyunjaya, 1994; Wen & Liang, 1994; Shim, Song, Kwon, & Chao, 1997):
- high stiffness (rigidity), (low passive compliance; which has negative effect in many industrial applications)
- high load to mass (weight) ratio
- better Dynamic performance (i.e. faster dynamic response) (Wang Y. , 2007)
- higher precision of the output controlled link, i.e. superior positioning capability
- lower natural frequency
- Accuracy over t he amplitude of motion
The closed mechanical chain makes it impossible to derive the explicit kinematic equations. Yang and Lee (Yang & Lee, On the Workspace of Mechanical Manipulators, 1983; Yang & Lee, Feasibility study of a platform type of robotic manipulators from a kinematic viewpoint, 1984) performed a kinematic feasibility study of the Stewart platform manipulator and made the first attempt towards its workspace analysis including the physical restrictions on the spherical joints. Considering a special architecture of the Stewart platform, they developed an algorithm for finding the section of the reachable workspace on a particular plane and provided a numerical evidence to the fact that the workspace and manoeuverability of parallel manipulators (and the Stewart platform in particular) is rather poor (Mruthyunjaya & Dasguptaa, 2000; Yang & Lee, On the Workspace of Mechanical Manipulators, 1983; Gogu, 2008).
Nonetheless closed kinematic link of parallel manipulators renders their workspace limited whereas a for an open-chained serial robot manipulator the workspace is only limited by the total length of its arm.
The first examples of a parallel manipulator were proposed in 1928 by J.E. Gwinnet which is illustrated in Figure 2 . Another early example was the two planes connected by legs with adjustable length by Gough (1956-1957) and by Gough and Whitehall (1962) as part of a tire-testing machine (Nair & Maddocks, 1994), as shown in Figure 3 . The moving platform, to which a tire is attached, is linked to the ground by 6 links with varying lengths. A universal joint is put at one of the ends of each link, a ball-and-socket joint at the other. Changing the length of the links modifies the position and the orientation of the moving platform, and therefore of the wheel. This wheel is driven by a conveyor belt and the mechanism allows the operator to measure the tire wear and tear under various conditions (Merlet, 2006).

Figure 1 A 6-6 SPS Stewart-Gough platform
The original Stewart platform was designed for flight simulation (Stewart, 1965; Mruthyunjaya & Dasguptaa, 2000; Dasgupta & Mruthyunjaya, 1994; Shim, Song, Kwon, & Chao, 1997) , as shown inFigure 4.
The mechanism of Gough and Whitehall was older and closer to the description of parallel manipulators, this manipulating structure has gained popularity among researchers as generalized Stewart platform or simply as 'the Stewart platform'. In recent years, some authors have referred to the mechanism as the Stewart-Gough Platform (SGP).
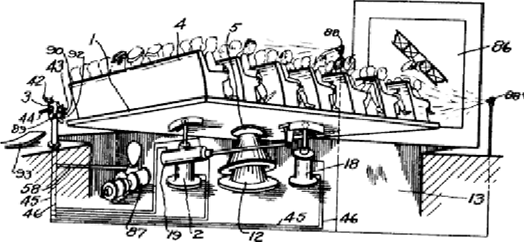
Figure2 The spherical mechanism proposed in 1928 by J.E. Gwinnet
Another early example of parallel robots was proposed by K. Cappel in 1967 for flight simulation. A drawing of his design is shown in Figure 5.Figure 6 show a modern flight simulators made as SGPs.

Figure 3 Gough platform (1947)
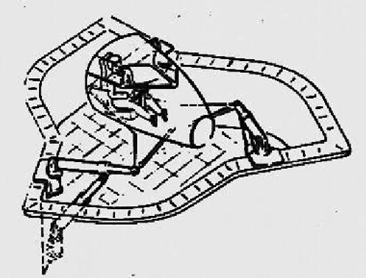
Figure4 Original Stewart platform sketch by Stewart (1965).
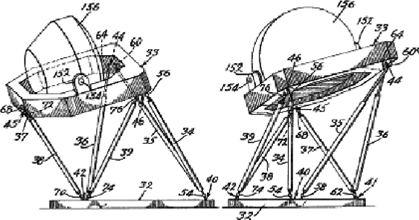
Figure5 A drawing in the patent of K. Cappel (1967).

Figure6 The Airbus A340 simulator.
(realization THOMSON-CSF, photograph by P. Palomba)
A problem with the serial robots is that as the length of a serial open-chained robot increased the bending moment caused by the load which it carries increases. As serial robots can be considered as cantilever structure, they vibrate at high speeds.
Open-chain serial manipulators possess both the advantages and the disadvantages of the human arm. Human arm like (anthropomorphic or Shi and Fenton Platform-Type) The above characteristics are obviously due to the fact their kinematic chain is closed and the load can be shared by the legs. For the case of SGP the kinematic precision can also be high. This is a result of the position of the platform being defined by six length parameters and lack of any redundancy. This type of manipulator is interesting because of its extreme redundancy, its large workspace is large and good load capacity/mass ratio: the LX4 mass is 120 kg for a transportable load of 75 kg (Merlet, 2006). However, such a robot is difficult to control. There are some manipulators which are called hybrid manipulators. They can be hybrid in the sense that they have features of both parallel and serial manipulators. An example of hybrid manipulators is shown in Figure 7 . There are undoubtedly other applications of SGPs, as Figure 8 shows a curious application of a hexapod design.

Figure7 The Logabex robot LX4, made by piling up left hands.
(photograph bykind permission of the Logabex company).

Figure8 Another application of hexapod design
(Jos´e Mar´ıa Sabater Navarro's thesis, 2003)
2. Singularities
As a consequence of the above facts, the manifestation of the duality between the two classes of manipulators continues in the context of singularity, which is associated with the degeneracy of the input-output relationships. The singularities of serial manipulators are associated with a loss in degrees of freedom (dof) and partial locking while the preponderant type of singularities of parallel manipulators is associated with a gain in dof and uncontrollability. Singular configuration: Special position of the robot links which implies a reduction of mobility of the end-effector (Gogu, 2008).
Every mechanism has singular positions in which the general equations for the motion of the mechanism do not hold. In series-connected manipulators, the singular positions result in the loss of one or more degrees of freedom. In parallel-connection manipulators, the singular positions result in the gain of one or more degrees of freedom. The search for singular positions has thus been reduced to the search for positions in which the six leg vectors are not linearly independent. This condition can be tested for by checking for singularities of the matrix of the Plucker line coordinates (Merlet, 2006) of the six legs. If the determinant of this matrix is zero, the manipulator is in a singular position.
The singular positions were studied by Fichter (Fichter, 1986). Singularities are classified into three categories:
· architecture
· configuration
· and formulation
The above cases are presented by Wolf and Shoham (Wolf & Shoham, 2003).
Amount by which the degree of freedom of a robot exceeds the number of independent variables that are necessary to define the task to be performed. Redundancy Existence of more than one means to accomplish a given function. Manoeuvrability Ability of a robot with redundant mobility to solve a task by using various combinations of movements of its links (Gogu, 2008).
In his keynote speech entitled “Still a long way to go on the road for parallel mechanisms” presented in ASME 2002 DETC Conference, Jean- Pierre Merlet from INRIA Sophia Antipolis, France, the author of the first books on parallel robots has stated:
“Synthesis of parallel robot is an open field (there is a very limited number of papers addressing this issue) and, in my opinion, one of the main issue for the development of parallel robots in practice”. The importance of design synthesis defined by structural and dimensional synthesis is also reiterated by J-P. Merlet (Merlet, 2006):
“ Synthesis of robots may be decomposed into two processes: structural synthesis (determine the general arrangement of the mechanical structure such as the type and number of joints and the way they will be connected) and dimensional synthesis (determine the length of the links, the axis and location of the joints, the necessary maximal joint forces/torques).
The performances that may be obtained for a robot are drastically dependent on both synthesis.” (Gogu, 2008).
3. Medical Applications
It is important to note medical applications of parallel manipulators. It is possible to use another advantage of parallel structures compared to their serial counterpart that they are much less sensitive to scaling effect, and are therefore appropriate for micro-robots. For medical applications this is appropriate for laparoscopy or Minimally Invasive Surgery (MIS) (especially endoscopy. Wendlandt built an endoscope active head made of a 3 degrees of freedom robot that is actuated by wires. Another solution for an endoscopic head with the Mips 3-d.o.f. robot is also suggested, which uses electrical motors. Such applications include Computer Aided Surgery in fields such as general (endoscopic) surgery, neurosurgeries (e.g. spinal surgery), ophthalmological surgery (yet on dogs!) and also in tele-surgery systems. A parallel micro-manipulator used in endoscopy is shown in Figure 9.Figure 10andFigure 11 illustrate two spinal surgery robots. A proposed design for an ophthalmologic surgery using a parallel robot is illustrated in Figure 12
Apart from the use of parallel structures in various medical fields, the kinematic of parallel structures are also used for a better understanding of the kinematics of complex human joints such as the knee or the shoulder complex, , for rehabilitation and sports training with the Caren platform of Motek _ MO and for mouth opening and closing training.
Figure 9throughFigure 16 demonstrate some of the clinical applications. Figure 13 shows a Hexapod 6 d.o.f. robotic treatment couch for patient positioning during radiation therapy (courtesy Medical Intelligence_ MI) with a 3 degrees orientation ability, 30 mm translation motion, a 0.1 mm resolution and a load of 185 kg.

Figure9 An MRI friendly 6-dof micro-manipulator, 2008.
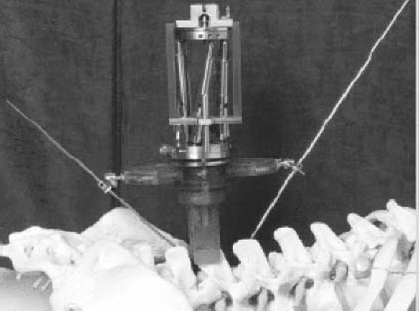
Figure10 The MARS/Spine Assist robot for spinal surgery.
(Mazor Surgical Technologies (Mazor Surgical Technologies))

Figure11 A parallel manipulator used in controlling of a spinal surgery precision robot
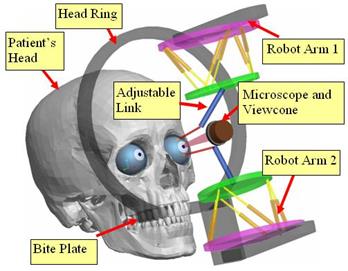
Figure12 An sketch for ophthalmologic surgery parallel robot (Design of Micro-Surgical Manipulators for Dual-arm Microsurgery)

Figure13 Romed surgical robot proposed by the Fraunhofer IPA.
(Merlet, 2006)
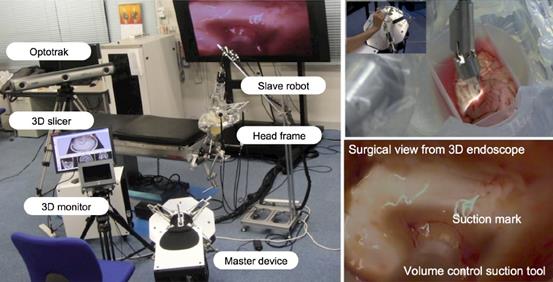
Figure 14 Intelligent neurosurgical instruments
(Intelligent neurosurgical instruments)
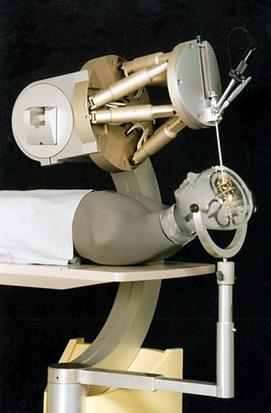
Figure 15 Custom Hexapod for brain surgery. Photo courtesy of IPA
(Hexapods / Motorized Micropositioning Stages & Actuators)
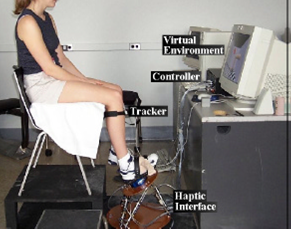
Figure16 Orthopaedic Rehabilitation Using the “Rutgers Ankle” Interface
(Deutsch, Latonio, Burdea, & Boian, 2001)
4. Redundancy
Figure 17 show a parallel robot with 9 legs called a nanopod , of which 3 are obviously providing redundancy. Links 1 to 6 are actuated, and links 7-9 are passive and only useful for the direct kinematics (Physik Instrumente).

Figure17 A 6 degrees of freedom parallel robot with 9 legs.
5. Forward and inverse kinematics
The problem of forward kinematics of parallel manipulators is the problem of finding the position and orientation of the mobile platform when the strut lengths are given. This problem has no known closed form solution for the most general 6-6 form of hexapod manipulator (with six joints on the base and six on the mobile platform) (Jakobovic & Jelenkovic, 2002).
The forward kinematics problem of the Stewart Platform Mechanism (SPM) does not have a unique solution since it involves solving a polynomial of order 16 (Yurt, Yanli, & Ozkol, 2007). Owing to their coupled and closed kinematic loops, forward kinematics is one of the most challenging problems in the area of parallel manipulators (Wang Y. , 2007).
Its closed kinematics chain which provide high mechanical stiffness also present an extremely difficult theoretical problem for forward kinematic and dynamic analysis. This problem is an impediment to the development of practical control algorithms capable of real-time trajectory generation, a necessity for industrial application of the manipulator.
The closed mechanical chain makes it impossible to derive the explicit kinematic equations. Since there is no explicit expression available for the forward (Liu, Lewis, Lebret, & Taylor, 1993), a majority of the studies reported are concerned with the direct (forward) position kinematics of the manipulator (Lee & Shim, 2001; Jakobovic & Jelenkovic, 2002; Yurt, Yanli, & Ozkol, 2007; Rolland & Chandra, 2009; Wu, Wu, & Yu, 2008; Husty, 1996; Raghavan, 1993; Wang, Hao, & Chen, 2008; Wohlhart, 1994; Dasgupta & Mruthyunjaya, 1994). Some of them attempt to solve the problem numerically while others aim at closed-form solutions to certain special cases (Dasgupta & Mruthyunjaya, 1994; Innocenti & Parenti-Castelli, 1991; Ji & Wu, 2001). Essentially, this problem requires the inversion of a set of nonlinear functions that define the leg lengths in terms of the configuration variables (Nair & Maddocks, 1994).
6. Summary
This article included a brief and general introduction to parallel manipulators, called the Stewart platforms or the Stewart-Gough platforms, its origin and its various applications. The important issue of singularity SGPs was briefly introduced. Since the TSF is an example of medical application of the parallel platforms, attempt was made to give a list of other medical applications of the SGP. As in many other engineering systems, the topic of redundancy is important in parallel robots, therefore it was also mentioned, despite the fact that TSF does not have redundancy, however it could not be ruled out as a possibility in future designs. Finally, the most important problem in SGPs, namely forward kinematics was outlined, which is the subject of the article that follows.
References
-
Dasgupta, B., & Mruthyunjaya, T. S. (1994). A Canonical Formulation of The Direct Position Kinematics Problem for A General 6-6 Stewart Platform. Mech. Mach. Theory, 29 (6), pp. 819--827.
-
Design of Micro-Surgical Manipulators for Dual-arm Microsurgery . (n.d.). (University of Columbia) Retrieved from Advanced Robotics and Mechanism Applications: http://www.columbia.edu/cu/mece/arma/projects/Eye%20surgery/Eyesurgery.shtml
-
Deutsch, J. E., Latonio, J., Burdea, G., & Boian, R. (2001). Rehabilitation of Musculoskeletal Injuries Using the Rutgers Ankle Haptic Interface: Three Case Reports. oceedings of EuroHaptics 2001 Conference.
-
Fichter, E. F. (1986). A Stewart Platform- Based Manipulator- General Theory and Practical Construction. The International Journal of Robotics Research, 5, pp. 157-182.
-
Gogu, G. (2008). Structural Synthesis of Parallel Robots Part 1: Methodology. Springer.
-
Guo, H. B., & Li, H. R. (2006). Dynamic analysis and simulation of a six degree of freedom Stewart platform manipulator. Proc. IMechE Part C: J. Mechanical Engineering Science, 220 , pp. 61-72.
-
Gürenci, B., Sarigül, A. S., & Karagülle, H. (2007). Kinematic and Kinetic Considerations on a Stewart Platform in Terms of Workspace. The 5th IFAC Intl. WS DECOM-TT , (pp. 191-196).
-
Hexapods / Motorized Micropositioning Stages & Actuators . (n.d.). (PI Precision Motion Control Solutions) Retrieved from Micropositioning: Motorized Linear Stages, Rotary Stages, Actuators: physikinstrumente.com/en/products/micropositioning_hexapod/micropositioning_experience.php
-
Husty, M. L. (1996). An Algorithm for Solving Direct Kinematics of General Stewart-Gough Platform. Mech. Mach. Theory, 31(4), pp. 365-380.
-
Innocenti, C., & Parenti-Castelli, V. (1991). A new kinematic model for the closure equation of the generalized Stewart platform mechanism. 26, pp. 247-252.
-
Intelligent neurosurgical instruments . (n.d.). (Nagoya Institute of Technology) Retrieved from Nagoya Institute of Technology: http://arata.web.nitech.ac.jp/
-
Jakobovic, D., & Jelenkovic, L. (2002). The forrward and inverse kinematics problems for Stewart parallel mechhanisms. http://www.zemris.fer.hr/~leonardo/unofficial/radovi/cim2002.pdf.
-
Ji, P., & Wu, H. (2001, Aug.). A Closed-Form Forward Kinematics Solution for the 6–6p Stewart Platform. IEEE Transactions on Robotics and Automation, 17(4), pp. 522-526.
-
Lee, J. D., & Geng, Z. (1993). A Dynamic Model of a Flexible Stewart Platform. Computers & Structures, 48 (3), pp. 367-374.
-
Lee, T. Y., & Shim, J. K. (2001). Forward kinematics of a general 6-6 Stewart platform using algebraic elimination. Mechanism and Machine Theory, 36, pp. 1073-1085.
-
Lenarčič, J., & Wenger, P. (2008). Advances in robot kinematics: Analysis and Design. Springer.
-
Liu, K., Lewis, F., Lebret, G., & Taylor, D. (1993). The Singularities and Dynamics of a Stewart Platform Manipulator. Journal of Intelligent and Robotic Systems, 8 , pp. 287-308.
-
Liu, M. J., Li, C. X., & Li, C. N. (2000, Feb.). Dynamic Analysis of the Gough-Stewart Platform Manipulator. IEEE Transactions on Robotics and Automations, 16 (1), pp. 94-98.
-
Mazor Surgical Technologies . (n.d.). Retrieved from Mazor Robotics: http://www.mazorrobotics.com/
-
Merlet, J. P. (2006). Parallel Robots, 2nd ed. Springer.
-
Mruthyunjaya, B., & Dasguptaa, T. S. (2000). The Stewart platform manipulator: a review. Mechanism and Machine Theory, 35 , pp. 15-40.
-
Mukherjee, P., Dasgupta, B., & Mallik, A. K. (2007). Dynamic stability index and vibration analysis of a flexible Stewart platform, Journal of Sound and Vibration. Journal of Sound and Vibration, 307, pp. 495–512.
-
Nair, R., & Maddocks, J. H. (1994). On the Forward Kinematics of Parallel Maipulators. The International Journal of Robotics Research, 13, pp. 171-187.
-
Raghavan, M. (1993, Jun.). The Stewart Platform of General Geometry Has 40 Configurations. Journal of Mechanical Design, 115(277-282).
-
Rolland, L., & Chandra, R. (2009). Forward Kinematics of the 6-6 general Parallel Manipulator Using Real Coded Genetic Algorithms. IEEE/ASME International Conference on Advanced Intelligent Mechatronics. IEEE/ASME.
-
Shim, J. H., Song, S. K., Kwon, D. S., & Chao, H. S. (1997). Kinematic Feature Analysis of a 6-Degree-of-Freedom In-Parallel Manipulator for Micro-Positioning. Proc. IROS 97 IEEE (0-7803-4119-8/97).
-
Stewart, D. (1965). A platform with six degrees of freedom. Proceedings of Institute of Mechanical Engineers, 180 (15), pp. 371-386.
-
Wang, X. S., Hao, M. L., & Chen, Y. H. (2008). On the use of differential evolution for forward kinematics of parallel manipulators. Applied Mathematics and Computation, 205 , pp. 760–769.
-
Wang, Y. (2007). A direct numerical solution to forward kinematics of general Stewart-Gough Platforms. Robotica, 25, pp. 121–128.
-
Wen, F., & Liang, C. (1994). Displacement Analysis of the 6-6 Stewart Platform Mechanism. Mech. Mash. Theory, 29(4), pp. 547-557.
-
Wohlhart, K. (1994). Displacement Analysis of the General Spherical Stewart Platform. Mech. Mach. Theory, 29 (4), pp. 581-589.
-
Wolf, A., & Shoham, M. (2003, Sept.). Investigation of Parallel Manipulators Using Linear Complex Approximation. Journal of Mechanical Design, 125, pp. 564-572.
-
Wu, P., Wu, C., & Yu, L. (2008). An Method for Forward Kinematics of Stewart Parallel Manipulators. ICIRA, Part I, LNAI 5314, (pp. 171–178).
-
Yang, D. H., & Lee, T. W. (1983). On the Workspace of Mechanical Manipulators. Journal of Mechanisms, Transmission and Automation Design, 105 , pp. 62-69.
-
Yang, D. H., & Lee, T. W. (1984). Feasibility study of a platform type of robotic manipulators from a kinematic viewpoint. Trans. ASME, J. Mech. Transm. Automn Des., 106 , pp. 191-198.
-
Yurt, S. L., Yanli, E., & Ozkol, I. (2007). Forward kinematics analysis of the 6-3 SPM by using neural Networks. Meccanica, 42, pp. 187–196.